자연계 수능·논술 해결을 위한 수학적 전략
쌓을 적(積) 나눌 분(分)-「함수」편
적분이라는 말은 쌓을 적(積)자와 나눌 분(分)자로 되어있다.
즉,적분은 "나누어서 쌓는다.
"는 개념으로 곡선으로 둘러싸인 넓이를 내접 또는 외접하는 직사각형의 무한 합으로 정의한다.
그러나 수학 교과서에서 배운 것처럼 꼭 직사각형들의 넓이로만 곡선으로 둘러싸인 넓이를 구하지 않았다.
그 예로,원에 내접하는 정사각형,정팔각형,정십육각형,... ,정n각형을 그려 보면, n의 값이 커질수록 정다각형의 넓이는 원의 넓이에 점점 가까워짐을 알 수 있다.
고대 그리스인들은 원의 넓이를 이와 같은 방법으로 구하였다고 한다.
이 방법을 실진법(悉盡法 ; 悉(모두),盡(없어지다),method of exhaustion)이라고 한다.
또한 아르키메데스(Archimedes: 287 - 212 B.C.)는 당시의 수학자 에라토스테네스(Eratosthenes: 275 - 194 B.C.)에게 보내는 편지 형식으로 쓴 저서 '방법론'에서 실진법을 이용하여 포물선과 직선으로 둘러싸인 부분의 넓이를 구하였다.
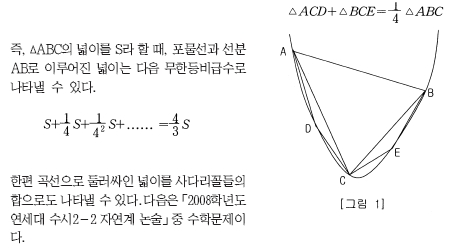
실진법은 [그림 1]과 같이 포물선과 선분 AB로 이루어진 넓이를 구하기 위하여 선분 AB와 평행선 접선의 접점을 C라 하고,선분 AC,CB에 평행한 접선의 접점을 D,E라 할 때,다음 등식을 이용하여 포물선과 직선으로 둘러싸인 부분의 넓이를 구하는 방법이다.
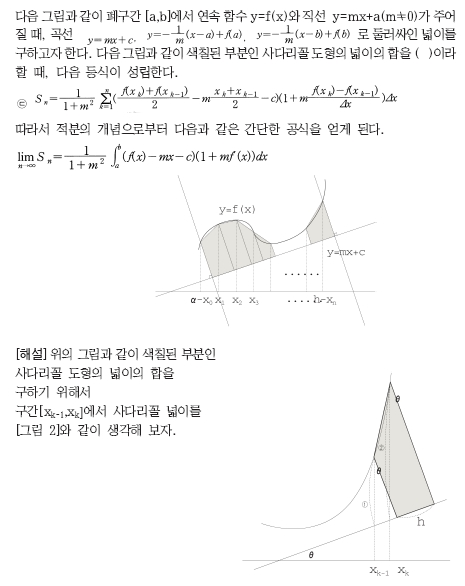
1-3 등식 ㉢이 성립함을 증명하시오. (15점)
[참고자료] 2008학년도 연세대 수시2-2 자연계 논술, 고등학교 교과서 수학2, 중앙교육진흥연구소
--------------------------------------------------------------
ⓒ 한국경제신문, 무단 전재 및 재배포 금지
쌓을 적(積) 나눌 분(分)-「함수」편
적분이라는 말은 쌓을 적(積)자와 나눌 분(分)자로 되어있다.
즉,적분은 "나누어서 쌓는다.
"는 개념으로 곡선으로 둘러싸인 넓이를 내접 또는 외접하는 직사각형의 무한 합으로 정의한다.
그러나 수학 교과서에서 배운 것처럼 꼭 직사각형들의 넓이로만 곡선으로 둘러싸인 넓이를 구하지 않았다.
그 예로,원에 내접하는 정사각형,정팔각형,정십육각형,... ,정n각형을 그려 보면, n의 값이 커질수록 정다각형의 넓이는 원의 넓이에 점점 가까워짐을 알 수 있다.
고대 그리스인들은 원의 넓이를 이와 같은 방법으로 구하였다고 한다.
이 방법을 실진법(悉盡法 ; 悉(모두),盡(없어지다),method of exhaustion)이라고 한다.
또한 아르키메데스(Archimedes: 287 - 212 B.C.)는 당시의 수학자 에라토스테네스(Eratosthenes: 275 - 194 B.C.)에게 보내는 편지 형식으로 쓴 저서 '방법론'에서 실진법을 이용하여 포물선과 직선으로 둘러싸인 부분의 넓이를 구하였다.
실진법은 [그림 1]과 같이 포물선과 선분 AB로 이루어진 넓이를 구하기 위하여 선분 AB와 평행선 접선의 접점을 C라 하고,선분 AC,CB에 평행한 접선의 접점을 D,E라 할 때,다음 등식을 이용하여 포물선과 직선으로 둘러싸인 부분의 넓이를 구하는 방법이다.

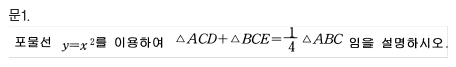
--------------------------------------------------------------

'논술자료' 카테고리의 다른 글
| [논술 길잡이] 권호걸의 통합논술 뽀개기 (0) | 2008.03.29 |
|---|---|
| [오태민의 마중물 논술] 철야 학원이 성업하지 않는 진짜 이유 (0) | 2008.03.29 |
| [영화와 논술] 아스테릭스/'위대한 영웅' 시저, 프랑스 영화에선 조연일 뿐 (0) | 2008.03.27 |
| '목화 스파이' 문익점? 그는 단지 '농림가'였다 (0) | 2008.03.27 |
| 위작 사기꾼 반 메헤렌, 독일 속인 국민적 영웅 되다 (0) | 2008.03.27 |