[스크랩] [술술 논술] 수학 80점 영어 85점, 어느 과목 더 잘했나

 

◆통계자료의 이해와 활용 / 표준 정규분포◆

9등급제는 구간척도(stanine)를 따르고, 구간척도에서는 표준정규분포를 동일한 간격으로 9개로 나눠 각 등급으로 삼는다. 따라서 9등급제 비율이 어떻게 결정되는지 알려면 정규분포 중에서도 표준정규분포를 이해해야 한다.

▶표준정규분포

기말고사 결과 A학생이 수학 80점, 영어 85점을 받았다. 어떤 과목을 더 잘한 것일까? 평균과 표준편차를 공부했다면 위 수치만으로는 어떤 과목을 잘했는지 판단할 수 없음을 알 것이다. 학교 전체의 수학 평균이 60점, 표준편차가 10점, 영어 평균이 80점, 표준편차가 5점이라고 하고 두 과목의 점수를 비교해 보자.

지난주에 살펴봤듯이 정규분포에서는 평균이 정규곡선의 위치를 결정하고 표준편차가 곡선의 모양을 결정한다. 따라서 평균과 표준편차가 다른 경우에는 두 분포를 비교하기 어렵다. 또한 특정한 정규분포에서는 원하는 확률을 계산하기가 쉽지 않다. 이러한 이유 때문에 평균과 표준편차를 표준화한 표준정규분포가 필요하다.

표준정규분포에서는 어떤 관찰값 X가 평균(ｍ)으로부터 표준편차(σ)의 몇 배 정도나 떨어져 있는가를 다음과 같이 표준화된 확률변수 Z로 나타낸다.

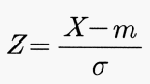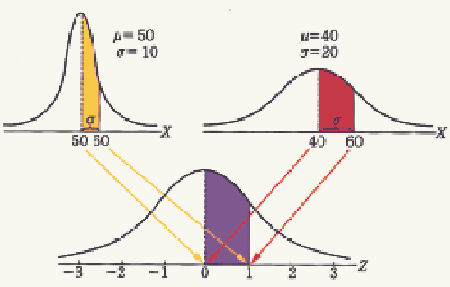
확률변수 Z의 분포는 항상 평균 ｍ=0, 분산 σ2＜윗첨자＞=1이 된다. 따라서 정규분포 N(0, 1)을 따를 때 표준정규분포가 된다고 할 수도 있다. [그림 1]은 평균과 표준편차가 다른 두 정규분포를 표준정규분포로 표준화했을 때의 곡선의 변화를 나타낸다.

이제 A학생의 수학과 영어 점수를 Z로 바꾸어 비교해 보자.

두 수치를 비교해 보면, 표준정규분포 곡선 상에서 수학 점수가 영어 점수보다 오른쪽에 위치하게 됨을 알 수 있다. 이로써 A학생은 영어보다 수학을 더 잘 봤다고 할 수 있다.

[정재원 대성논술아카데미 수석연구원]

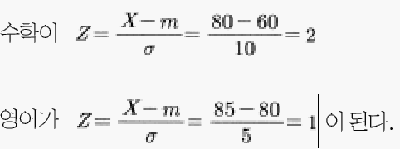출처 : 별먹는 빛

글쓴이 : 설경 원글보기

메모 :